En el inmenso universo de los datos, donde cada cifra narra una historia y cada variable guarda un misterio, los histogramas surgen como héroes discretos. Actúan como cartógrafos de la estadística, delineando el terreno de nuestros datos para facilitar su comprensión.
Un histograma es mucho más que un gráfico ordinario. Actúa como una ventana hacia la naturaleza fundamental de nuestros datos. Nos facilita la visualización de la distribución de una variable numérica y descubre patrones que podrían permanecer ocultos. Los picos y depresiones en un histograma nos informan sobre la concentración, dispersión y simetría de los datos.
Pero, ¿qué hace que los histogramas sean tan especiales? Principalmente, su simplicidad. No es necesario ser un experto en estadísticas para comprender un histograma; su lenguaje es universal y accesible para todos, desde estudiantes de secundaria hasta científicos de datos.
Además, los histogramas son extremadamente versátiles. Se pueden adaptar a cualquier conjunto de datos, independientemente de su tamaño o complejidad, y son una herramienta estadística fundamental para visualizar la distribución de los datos. Sus principales aplicaciones son:
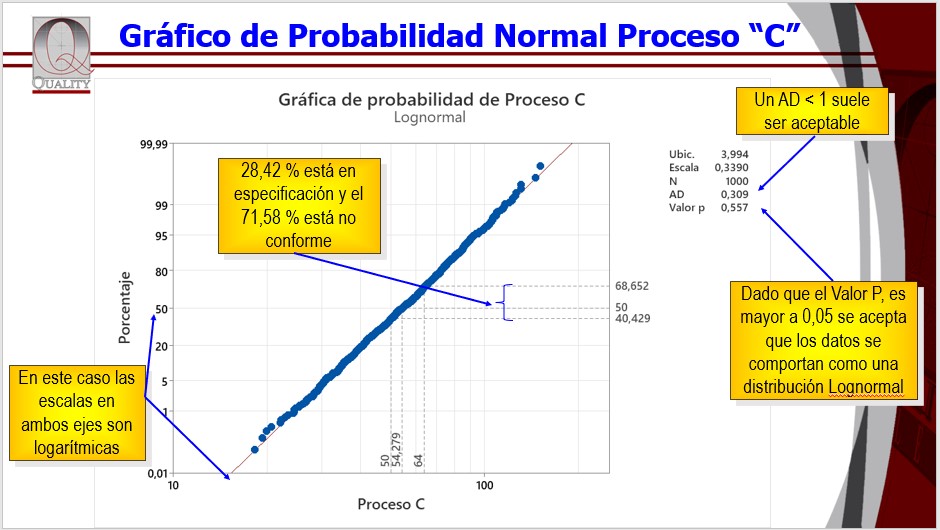
1. Visualización de la distribución de datos: El histograma revela cómo se distribuyen los datos, indicando si la distribución es simétrica, sesgada, si presenta picos o es uniforme. La distribución ilustrada parece ser Lognormal, caracterizada por un sesgo hacia valores bajos, lo cual es común al analizar los Tiempos de Ciclo.
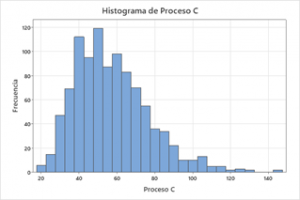
2. Identificación de patrones y tendencias: Los histogramas son útiles para discernir patrones y tendencias en los datos, tales como la aparición de valores atípicos o la agrupación de datos en rangos específicos. En el gráfico, es probable que los períodos de inactividad del proceso no sean relevantes para el objetivo del análisis.
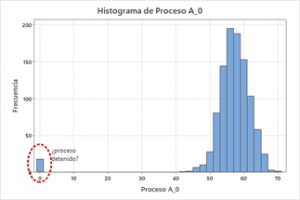
3. Estimación de la densidad de probabilidad: Utilizar un histograma permite estimar la densidad de probabilidad de una variable, facilitando el modelado de la distribución de datos. La función de densidad de probabilidad (FDP) es fundamental en la teoría de probabilidad y estadística para variables aleatorias continuas, indicando la probabilidad relativa de que una variable aleatoria asuma un valor determinado en un intervalo continuo. La FDP es invariablemente no negativa y su integral a lo largo de su dominio es igual a uno, asegurando que la variable aleatoria adquirirá algún valor dentro del rango establecido. Prácticamente, la probabilidad de que la variable esté en un intervalo específico se determina por el área bajo la curva de la FDP dentro de los límites de dicho intervalo. Anteriormente, esta área se calculaba mediante tablas, pero hoy en día, programas estadísticos como Minitab facilitan este proceso con el Gráfico de Probabilidad, tema que se abordará en otra sesión y que simplifica significativamente su cálculo.

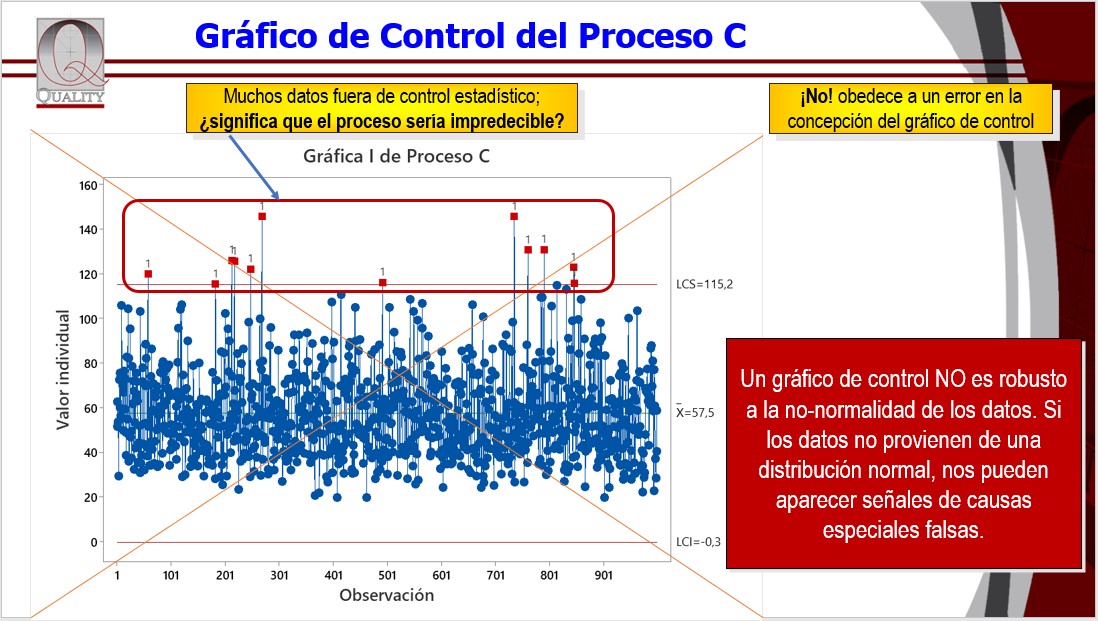
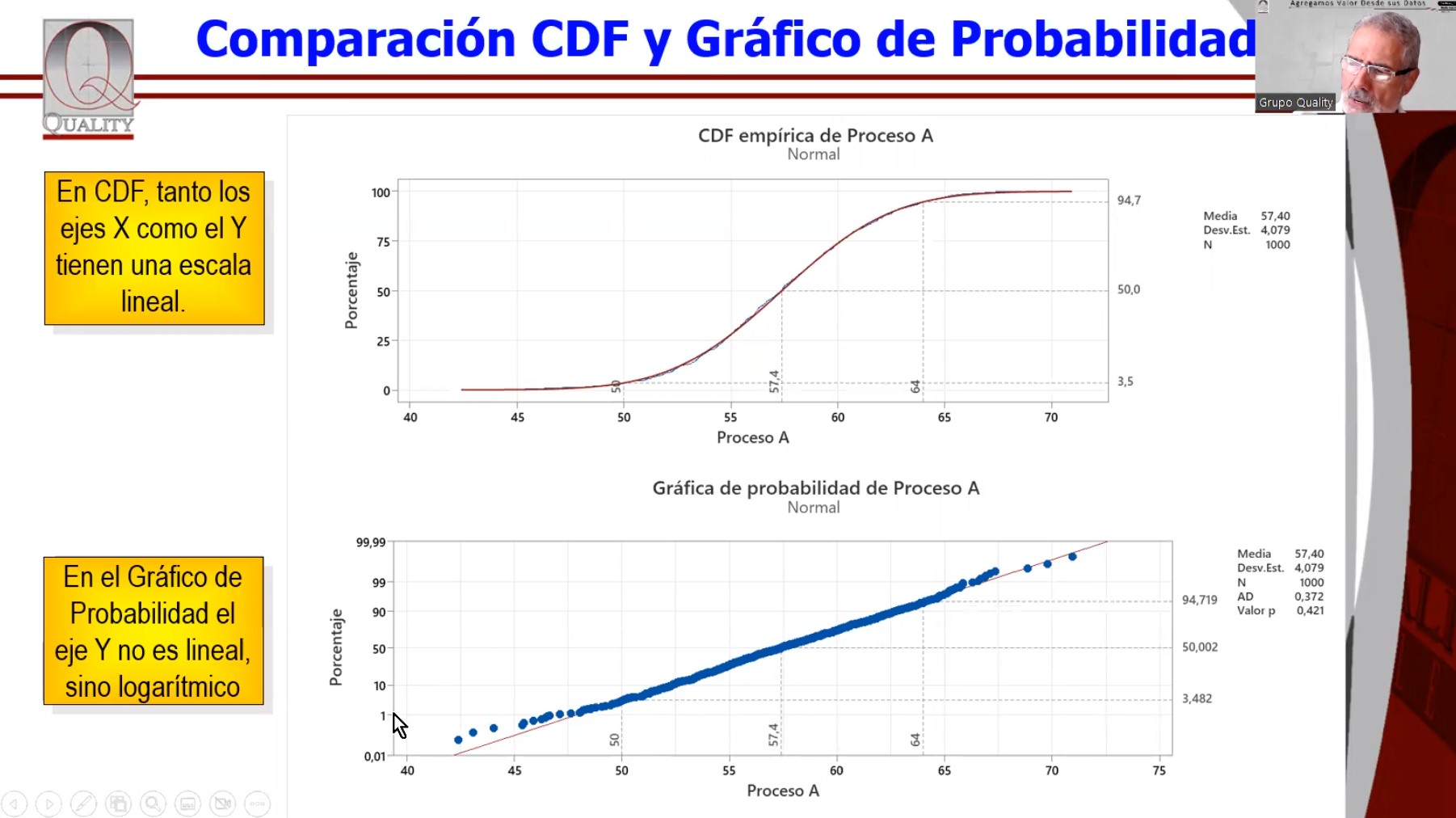
4. Comparación de distribuciones: Los histogramas son útiles para comparar las distribuciones de distintos conjuntos de datos. Esto permite analizar la dispersión de los datos o identificar si las distribuciones no se ajustan a lo esperado, lo que sugeriría la necesidad de una transformación de los datos. En el gráfico subsiguiente, si se espera que ambos procesos tengan un comportamiento similar y no es así, indica un problema. Las dispersiones son muy distintas y en particular, el “proceso C” parece exhibir una distribución no normal, a pesar de que las medias de ambos procesos parezcan cercanas.

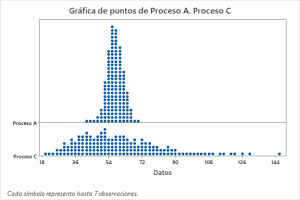
5. Gráfico de Puntos: Como alternativa al histograma, el gráfico de puntos resulta más útil cuando los datos son escasos o cuando se presentan valores atípicos o aislados que no se distinguen claramente en el histograma. Aunque con un volumen grande de datos, el histograma y el gráfico de puntos tienden a ser similares, el gráfico de puntos sigue siendo una herramienta valiosa para identificar valores atípicos. Por ejemplo, en el gráfico presentado, es posible que un valor superior a 144 en el “proceso C” no sea fácilmente perceptible en un histograma. En este caso, cada punto puede representar hasta siete observaciones, aunque también podría representar un único dato o cualquier cantidad entre uno y siete.
Se espera que sea evidente que el uso de histogramas en el análisis básico de procesos aporta un valor considerable para aquellos que desean mejorar la eficiencia y calidad de sus operaciones. Los histogramas facilitan la visualización de la distribución de los datos de forma clara y entendible, lo que ayuda a identificar patrones, tendencias y áreas potenciales de mejora. Mediante esta herramienta, los usuarios pueden adoptar decisiones informadas basadas en datos sólidos, propiciando una mejora continua de los procesos. El empleo de histogramas también promueve una cultura de análisis y mejora constante, lo que permite a los equipos trabajar de manera más eficiente y colaborativa. En definitiva, los histogramas no solo hacen más accesible el análisis de datos, sino que también promueven la innovación y el desarrollo en cualquier organización.
En publicaciones futuras, seguiremos discutiendo algunas de las herramientas abordadas en nuestros cursos básicos, centrados en el uso de herramientas estadísticas para mejorar la productividad de sus procesos operativos o transaccionales, aportando así valor al negocio.




Leave A Comment